Introduction to the rpact Package

Gernot Wassmer

November 13, 2025

Overview 📦

• Comprehensive validated R package implementing methodology described in Wassmer and Brannath (2016), second edition published in Sep. 2025
• Enables the design of traditional and confirmatory adaptive group sequential designs
• Provides interim data analysis and simulation including early efficacy stopping and futility analyses
• Enables sample-size reassessment with different strategies
• Enables treatment arm selection in multi-stage multi-arm (MAMS) designs
• Enables subset selection in population enrichment designs
• Provides a comprehensive and reliable sample size calculator

Developed by RPACT 🏢

• RPACT company founded in 2017 by Gernot Wassmer and Friedrich Pahlke
• Idea: open source development with help of “crowd funding”
• Currently supported by 21 companies
• \(>\) 80 presentations and training courses since 2018, e.g., FDA in March 2022
• 29 vignettes based on Quarto and published on rpact.org/vignettes
• 28 releases on CRAN since 2018

RCONIS 🚀

• Grow RPACT company to offer a wider range of services
• Statistical consulting and engineering services: Research Consulting and Innovative Solutions
• Joint venture between RPACT GbR (rpact.com) and inferential.biostatistics GmbH (inferential.bio) founded by Daniel Sabanés Bové and Carrie Li
• Website: rconis.com

The R Package rpact – Functional Range

Trial Designs 🔬

• Fixed sample designs:
  • continuous, binary, count, survival outcomes
• Group sequential designs:
  • efficacy interim analyses, futility stopping, alpha-spending functions
• Adaptive designs:
  • Inverse normal and Fisher’s combination test, conditional error rate principle
  • Provides adjusted confidence intervals and bias corrected estimates
  • Multi-arm multi-stage (MAMS) and enrichment designs, sample size reassessment

Easy to understand R commands:

getDesignGroupSequential()
getDesignInverseNormal()
getDesignFisher()
getDesignConditionalDunnett()

Sample Size and Power Calculation 💻

Sample size and power can be calculated for testing:

• means (continuous endpoint)
• proportions (binary endpoint)
• hazards (survival endpoint)
  • Note: flexible recruitment and survival time options
• rates (count endpoint)

Easy to understand R commands:

getSampleSize[Means / Rates / Survival / Counts]()
getPower[Means / Rates / Survival / Counts]()

Example: Sample Size Calculation 🧮

# Define the design.
getDesignGroupSequential(
    typeOfDesign = "asOF",
    futilityBounds = c(0, 0)
) |>
    # Perform sample size calculation.
    getSampleSizeMeans(
        alternative = 2,
        stDev = 5
    ) |>
    # Obtain summary.
    summary()

Sample size calculation for a continuous endpoint

Sequential analysis with a maximum of 3 looks (group sequential design), one-sided overall significance level 2.5%, power 80%. The results were calculated for a two-sample t-test, H0: mu(1) - mu(2) = 0, H1: effect = 2, standard deviation = 5.

Stage	1	2	3
Planned information rate	33.3%	66.7%	100%
Cumulative alpha spent	0.0001	0.0060	0.0250
Stage levels (one-sided)	0.0001	0.0060	0.0231
Efficacy boundary (z-value scale)	3.710	2.511	1.993
Futility boundary (z-value scale)	0	0
Efficacy boundary (t)	4.690	2.152	1.384
Futility boundary (t)	0	0
Cumulative power	0.0204	0.4371	0.8000
Number of subjects	69.9	139.9	209.8
Expected number of subjects under H1			170.9
Overall exit probability (under H0)	0.5001	0.1309
Overall exit probability (under H1)	0.0684	0.4202
Exit probability for efficacy (under H0)	0.0001	0.0059
Exit probability for efficacy (under H1)	0.0204	0.4167
Exit probability for futility (under H0)	0.5000	0.1250
Exit probability for futility (under H1)	0.0480	0.0035

Legend:

• (t): treatment effect scale

Adaptive Analysis 📈

• Perform interim and final analyses during the trial using group sequential method or p-value combination test (inverse normal or Fisher)

• Calculate adjusted point estimates and confidence intervals (cf., Robertson et al. (2023), Robertson et al. (2025))

• Perform sample size reassessment based on the observed data, based on calculation of conditional power

• Some highlights:

  • Automatic boundary recalculations during the trial for analysis with alpha spending approach, including under- and over-running
  • Adaptive analysis tools for multi-arm trials and enrichment designs

Easy to understand R commands:

getStageResults()
getRepeatedConfidenceIntervals()
getAnalysisResults()

Simulation Tool 🧪

Obtain operating characteristics of different designs:

• Assessment of adaptive sample size recalculation strategies
• Assessment of treatment selection strategies in multi-arm trials
• Assessment of population selection strategies in enrichment designs

Easy to understand R commands:

getSimulation[MultiArm/Enrichment][Means/Rates/Survival/Counts]()

Example:

getSimulationMeans()
getSimulationMultiArmMeans()
getSimulationEnrichmentMeans()

\(\rightarrow\) rpact useful for conducting flexible simulations in clinical trial planning

User Concept – R generics

In general, everything runs with the R standard functions which are always present in R: R generics.

• Visualize:
  • print()
  • summary()
  • plot()
• Continue work:
  • as.data.frame()
  • length()
  • names()

User Concept – Most parameters have a default value

Example: getDesignInverseNormal() produces the output:

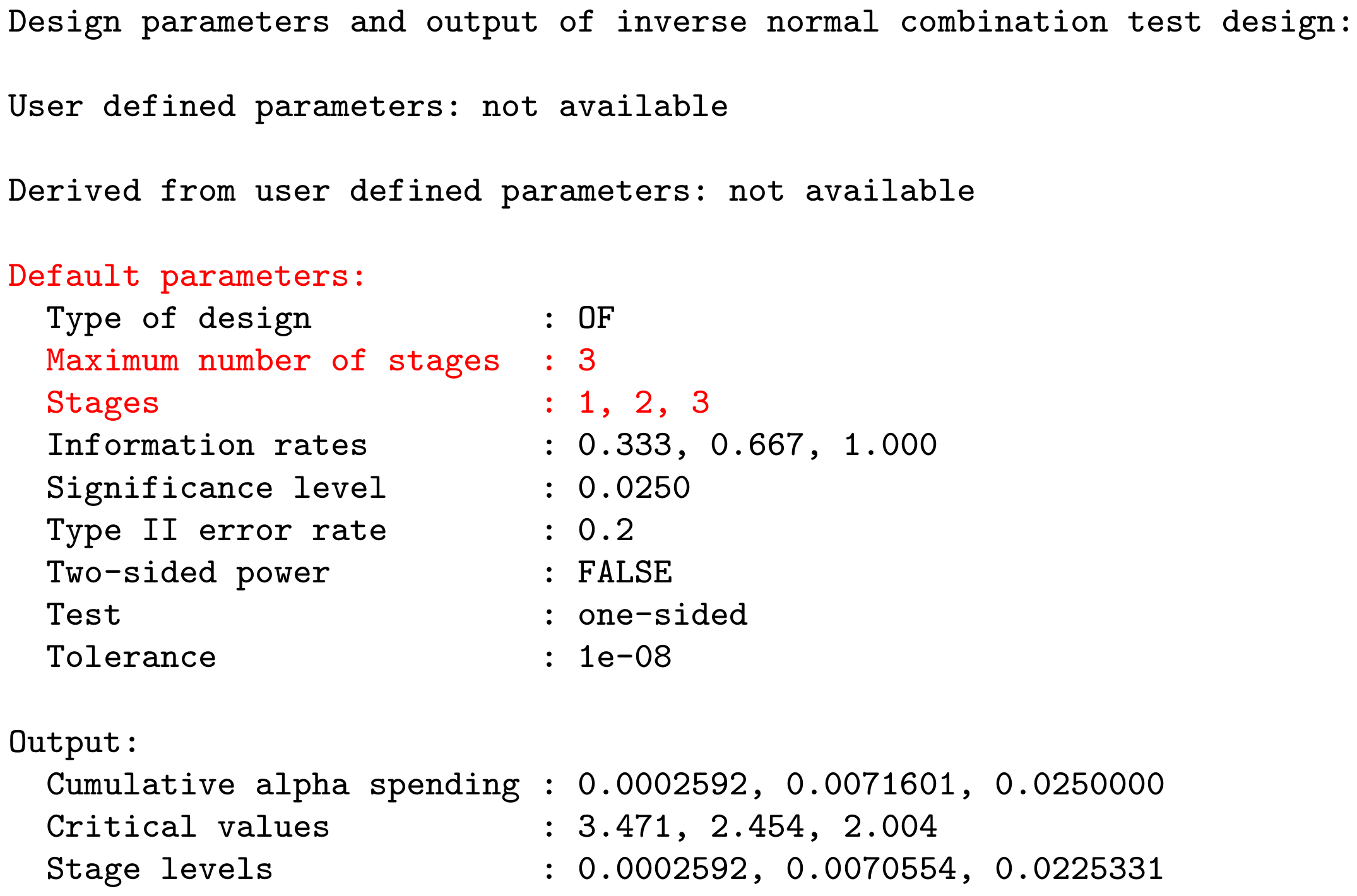
User Concept – Most parameters have a default value

Example: getDesignInverseNormal(kMax = 2) produces the output:

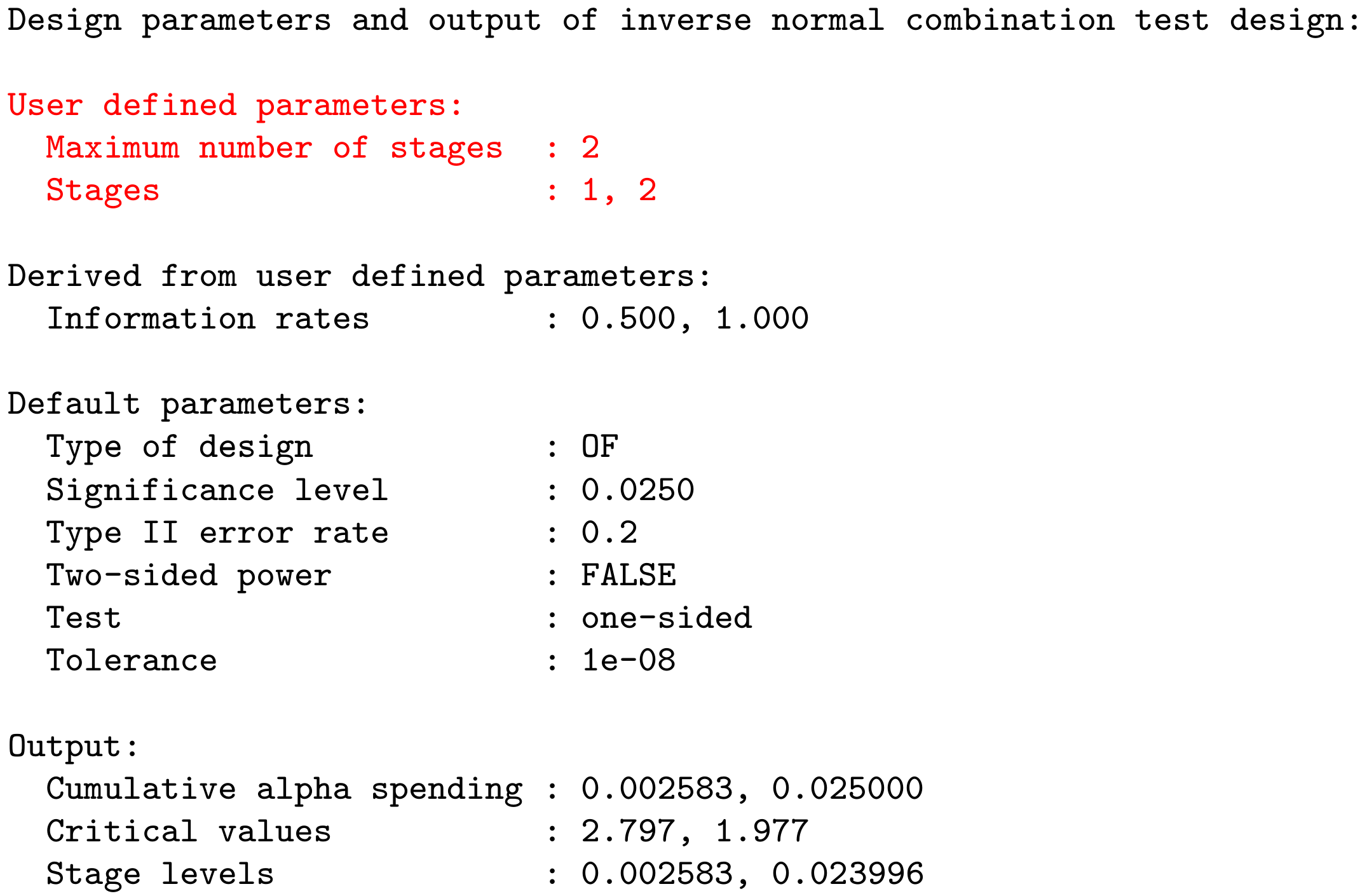
Recent Developments

Just in the near future you will see in rpact:

• Patient level survival data simulations for multi-arm and enrichment designs
• Optimum conditional error functions according to Brannath et al. (2024) (package optconerrf published on CRAN Sep 09, 2025)
• Least square means interface for continuous endpoints
• Additional futility boundary scales: function getFutilityBounds()
  • Available scales: zValue, pValue, conditionalPower, condPowerAtObserved, predictivePower, reverseCondPower, effectEstimate (cf., Ortega-Villa et al. (2025))

Second Edition of the Book

• Group Sequential and Confirmatory Adaptive Designs in Clinical Trials by Gernot Wassmer and Werner Brannath
• Second Edition (Springer, 2025) — published on September 24, 2025
• Now featuring numerous rpact R code examples demonstrating the methods implemented in the package
• For more information, visit: link.springer.com/book/10.1007/978-3-031-89669-9

The R Package rpact – Getting started

Various learning concepts available:

• Training, online or onsite: www.rpact.com/contact
• Vignettes: www.rpact.org/vignettes
• Graphical user interface RPACT Cloud: cloud.rpact.com

References

Brannath, W., M. Dreher, J. Verth, and M. Scharpenberg. 2024. “Optimal Monotone Conditional Error Functions.” arXiv Preprint arXiv:2402.00814.

Ortega-Villa, Ana M, Megan C Grieco, Kevin Rubenstein, Jing Wang, and Michael A Proschan. 2025. “Futility Monitoring in Clinical Trials.” Statistics in Medicine 44 (13-14): e70157.

Robertson, David S, Thomas Burnett, Babak Choodari-Oskooei, Munya Dimairo, Michael Grayling, Philip Pallmann, and Thomas Jaki. 2025. “Confidence Intervals for Adaptive Trial Designs I: A Methodological Review.” Statistics in Medicine 44 (18-19): e70174.

Robertson, David S, Babak Choodari-Oskooei, Munya Dimairo, Laura Flight, Philip Pallmann, and Thomas Jaki. 2023. “Point Estimation for Adaptive Trial Designs I: A Methodological Review.” Statistics in Medicine 42 (2): 122–45.

Wassmer, Gernot, and Werner Brannath. 2016. Group Sequential and Confirmatory Adaptive Designs in Clinical Trials. Springer. https://link.springer.com/book/10.1007/978-3-319-32562-0.